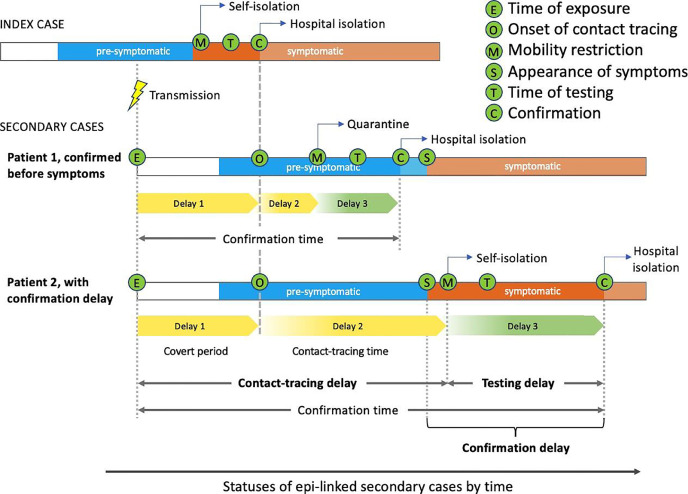
To investigate how the combination of NPIs contributed to suppression of the outbreak, we modelled the separate effects of social distancing interventions and changes in the efficiency of tracing and testing, by taking account of the relationship between the dynamics of transmission and confirmation delay.
Impact of interventions on Re
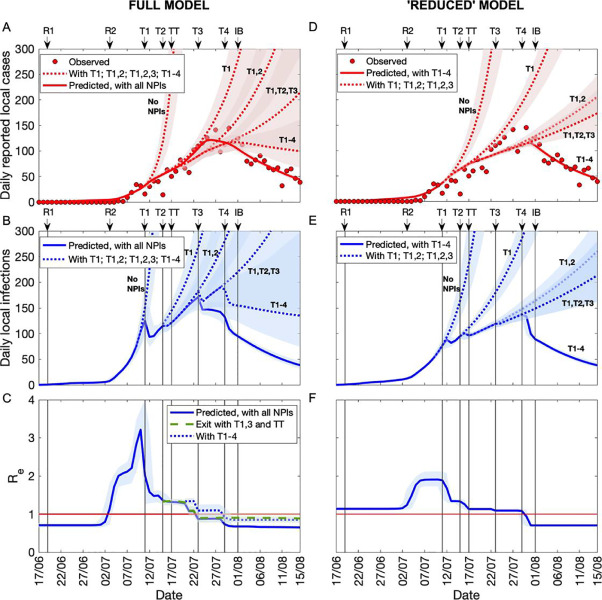
Table 1Dates of relaxation of social distancing measures and implementation of significant public health interventions. Effects (relative reduction) on Re are listed for NPIs deployed during the outbreak.
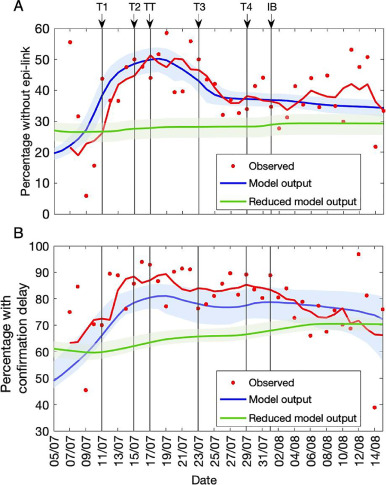
Fig. 4Comparisons between actual values and model projections for two indicators of reduced efficacy of tracing and testing, namely: (A) contact-tracing ineffectiveness (i.e. percentages of all local cases without an epi‑link) and (B) contact-tracing (or confirmation) inefficiency (i.e. proportion of epi‑linked cases with confirmation delay); In both graphs, red circles represent the observed proportion each day and the red curve is a moving average (5-day window, centred at day 3). The blue curve represents the model-derived output, while the green curve is the output of the ‘reduced’ model that did not incorporate the dynamics of delay. Credible intervals were generated by 400 repeated samplings from the posterior distributions.