Soli d–solid phase transitions can enhance energy transduction to drive actuation. For example, in shape memory alloys, phase transitions from martensite to austenite lead to changes in the lattice displacement, which have been harnessed to cause movement (1, 2). Similarly, phase transitions in liquid crystal elastomers, from well-aligned nematic states to randomly aligned isotropic states, have been used to drive motion (3⇓⇓⇓⇓–8). Such phase transitions can also change the mechanical properties of the material system. For example, liquid crystal elastomers can enter in a state of “semisoft elasticity,” where strain is accommodated at near-constant stress as the material transitions from one phase to another (4, 9). Transformations such as these offer desirable control of energy conversion (10, 11), which can be beneficial in dissipating energy and protecting the system from damage. While solid–solid phase transitions provide promise for energy-management devices, predictably engineering these transitions and their impact on material properties is challenging.
Mechanical metamaterials offer an opportunity to overcome this challenge (12, 13). Mechanical metamaterials use periodically arranged blocks, or “meta-atoms” (13), to mediate mechanical deformation, stress, and energy. They have been used to program stress–strain responses (14⇓–16), modulate elastic wave propagation (17⇓⇓⇓–21), and control energy dissipation (22, 23). Mechanical metamaterials typically rely upon internal geometric changes to introduce functionality, taking advantage of known nonlinear geometric mechanics for elastic materials (24, 25). This approach is widely adopted since analytical or numerical models can be readily derived to understand and predict the observed behaviors, thus providing pathways for systematic programming of the material’s response.
Further advantages may be realized by combining additional fields beyond elasticity (26). Recently, the addition of field-responsive materials to metamaterials has been demonstrated to offer advantageous functionality (27⇓⇓⇓–31). These demonstrations are impactful on their own, but more importantly, they introduce a broader paradigm with far-reaching implications. In particular, the combination of nonlinear fields, such as magnetic and electric, with orientationally dependent regimes of attraction and repulsion opens up the creation of “meta-atoms” that more closely reflect characteristics of atomic or molecular arrangements in materials phase structures (31). Accordingly, this counter play of nonlinear fields can be used to quantitatively define phase transitions in mechanical metamaterials composed of elastic and magnetic elements.
Here, we demonstrate the power of this paradigm by developing elasto-magnetic metamaterials that undergo phase transitions. These phase transitions, similar to enabling ones in shape memory alloys and liquid crystal elastomers, have beneficial changes in strain state and mechanical properties that can drive actuations and manage overall energy transduction. The metamaterial changes its constitutive response concurrently as the phase transitions happen, resulting in a nonmonotonic stress–strain relation. The reversible shift between the two phases significantly enhances the metamaterials’ dynamic performance, improving the energy release in dynamic recoil and mitigating the impact loading. Importantly, we introduce a Landau free energy framework to model the phase transitions for the elasto-magnetic metamaterials, which can be extended to metamaterials with other field-responsive materials or ones that are purely mechanical (20, 21). This framework creates opportunities based on fundamental principles for using phase transitions to control engineering performance at high rates.
Results
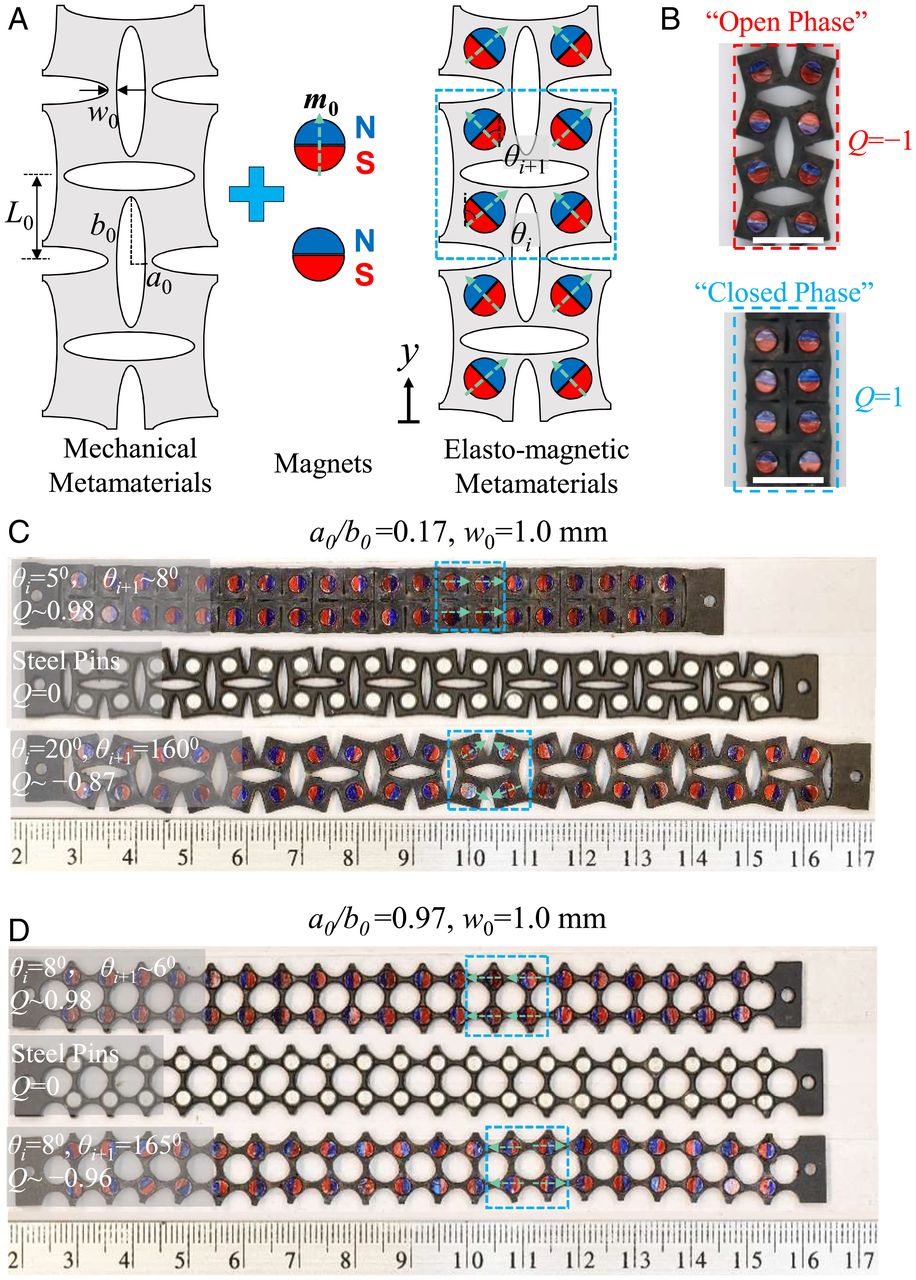
A schematic of the elasto-magnetic metamaterial is shown in Fig. 1A. For physical demonstrations, we fabricate the metamaterials from a polymeric sheet (PU 40A, McMaster-Carr) and cylindrical magnets that are magnetized along the diameter (Neodymium Magnet, McMaster-Carr). The magnet is 3.18 mm thick, 3.10 mm in diameter, and 0.18 g in weight. The thickness of the polymeric sheet (h) is also 3.18 mm. We laser cut (Universal Laser System, VSL 3.5) a pattern of orthogonally aligned pores into the polymeric sheet to create a polymeric network of “plates” connected by thin “ligaments.” We define the fabricated metamaterial structures with the semiminor and semimajor axes a0 and b0 of the pores, the ligament’s width between adjacent pores, w0. The length of a representative unit, L0 = w0 + b0 + a0, is fixed as 6 mm. Magnets with a diameter ∼3.1 mm and weight ∼0.18 g are embedded at the center of plates such that they are constrained by frictional contact with surrounding polymer. By embedding permanent magnets in mechanical metamaterials, a rich set of mechanical properties, including buckling strain (32, 33), postbuckling stiffness (32⇓–34), and multistability (35), have been finely tuned. Here, we reveal how magnetic domains, with nonlinear, orientationally dependent force interactions within elastic structures control reversible phase transitions and allow high–strain-rate properties to be programmed. The magnetic interactions are further programmed via the magnets’ orientations, defined by the angle between the magnetic moment and the y-axis, θi. We prescribe a mirror symmetry in the horizontal direction and control the magnetic interaction via the angles θi and θi+1 of the neighboring magnets (Fig. 1A). An orientational parameter is defined at the configuration free from external loadings, Q = cos(θi)cos(θi+1), representing the relative strength of magnetic interactions and ranging from −1 to 1. The neighboring magnets are repulsive when Q < 0 and switch to an attractive interaction as Q > 0. We replace the magnets with stainless-steel cylinders (thickness ∼3.18 mm, diameter ∼3.1 mm, and weight ∼0.18 g) to create metamaterials with Q = 0, labeled as neutral in Fig. 1 C and D (SI Appendix, section 1 for fabrication details).
Elasto-magnetic metamaterials composed of polymeric networks and interacting magnetic domains. (A) Interacting magnets are embedded in mechanical metamaterials with orthogonally aligned elliptical pores. The metamaterial structure is characterized by the ligament width, w0, and the semiminor and semimajor axes, a0 and b0. The magnets are magnetized through the diameter, with the color representing the two poles. The ith magnet is aligned at an angle θi between its magnetic moment and the y-axis. (B) Open and closed phases created by the repulsive and attractive magnetic domains, respectively (Scale bar, 10 mm). (C) Metamaterials with elliptical pores and attractive, neutral, and repulsive magnetic interactions (from Top to Bottom). (D) Metamaterials with circular pores and attractive, neutral, and repulsive magnetic interactions (from Top to Bottom).
We observe two stable phases, which we refer to as “open” and “closed” regarding the state of the metamaterial pores. An open phase is induced by a strong repulsive interaction between neighboring magnetic domains with Q = −1, while with Q = 1 a closed phase develops (Fig. 1B). The phase states also depend upon the geometry of the metamaterial. For example, for elliptical pores (a0/b0 = 0.17), the elasto-magnetic metamaterials support the open phase with Q = 0 and −1 and the closed phase at Q = 1 (Fig. 1C). In contrast, circular pores (a0/b0 = 0.97) only support an open phase for all Q-values (Fig. 1D).
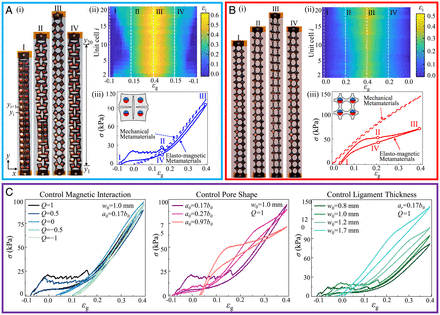
The equilibrium phase state can also be altered by the application of an external force. We apply a uniaxial tension to metamaterials with elliptical pores (a0/b0 = 0.17, Fig. 2A) and circular pores (a0/b0 = 0.97, Fig. 2B) under the attractive magnetic domains (Q = 1). Snapshots at different deformations (marked as I, II, III, and IV) are captured for both pore shapes. The configurational changes of the two structures are remarkably different (Movies S1 and S2). A closed-to-open phase transition emerges at the top and bottom ends in the metamaterial with elliptical pores. It propagates toward the center, changing the configuration to a homogeneous open phase as the deformation increases. The sample maintains the open phase in the unloading path, ending with a fast transition to the closed phase as the magnets snap to each other when a small separation distance is reached. By contrast, the metamaterial with circular pores preserves the open phase, deforming the ligaments in response to external forces.
Experimental observations of phase transitions in elasto-magnetic metamaterials. (A) Elasto-magnetic metamaterials with elliptical pores and attractive magnetic interactions. (i) The snapshots of metamaterials under quasistatic loading (I and II) and unloading (III and IV). The metamaterial is in a closed phase initially, and the open phase nucleates at the edges and propagates toward the center under the tensile loading. Upon unloading, the open phase transits back to the closed phase, starting from the center. (ii) The local strain increases from the edges to the center as a mixture of two phases emerges and becomes a homogeneous open phase. (iii) The stress–strain response of elasto-magnetic metamaterials (solid lines) and mechanical metamaterials (dashed lines) with the elliptical pores. (B) Elasto-magnetic metamaterials with circular pores and attractive magnetic interaction deform homogeneously under external loading, without a phase transition. (i) The snapshots of metamaterials under quasistatic loading (I and II) and unloading (III and IV). The metamaterial remains in an open phase without phase transitions. (ii) The local strain changes homogenously with the global strain across the metamaterial. (iii) The stress–strain response of elasto-magnetic metamaterials (solid lines) and mechanical metamaterials (dashed lines) with the circular pores. (C) The constitutive responses in elasto-magnetic metamaterials are programmed by magnetic interactions (Q = −1∼1) and the metamaterial geometry (the pore shape a0/b0 and the ligament thickness w0).
The phase transitions alter the relationship between the global and local strains, defined by the displacements between the neighboring magnets. The applied global strain, εg, and the local strain for the ith magnets in the vertical direction, εi, are the following:[1]where yi and Yi are the positions of the center of the ith magnet in the deformed and undeformed configuration, L0 is the length of the representative unit of the metamaterials, and n = 20 in our experiments. We plot the evolution of the local strain εi as a function of the global strain εg for metamaterials with both elliptical (Fig. 2A) and circular (Fig. 2B) pores. As the attractive magnetic interaction creates a closed phase in elliptical pores, the global strain is negative (εg∼−0.1) before applying external forces. In Fig. 2A, a discontinuous change of local strain is observed between stages I and II, propagating toward the center of the sample. The traveling boundary signifies a transition between the closed and open phases. The local strain becomes uniform and changes with the global strain as the sample is dominated by the open phase (between stages II and IV). For the circular pores in Fig. 2B, the open phase is preserved, and the global strain starts with a positive value due to the fluctuation induced by embedding the magnets into the polymer. The local strain is uniformly distributed, and it changes affinely with the global strain in the loading and unloading cycle.
The constitutive response of the elasto-magnetic metamaterial changes as the phase transitions occur. We compare the stress–strain curves for metamaterials with elliptical and circular pores (solid lines) and their elastic counterparts without magnets or stainless-steel cylinders (dashed lines, SI Appendix, Fig. S2B) in Fig. 2 A and B. In materials with elliptical pores (Fig. 2A), the attractive magnetic interaction induces an initial regime with a higher modulus than the metamaterial without magnetic domains. The transition from a closed to an open phase and the subsequent propagation of the phase interface results in a jagged state, with a plateau stress ∼20 kPa. For an open phase, the constitutive response in elasto-magnetic metamaterials is similar to that of metamaterials without magnets due to the weak magnetic interaction at a large distance. In addition, large hysteresis is observed in elasto-magnetic metamaterials with elliptical pores (Fig. 2A), which is negligible in the mechanical metamaterials or magnetic interactions alone (SI Appendix, Fig. S2). This is related to the differences in the phase transitions between the loading and unloading cycles. In circular pores (Fig. 2B), the magnetic interaction is weak at the open phase. The ligament’s constitutive response results in an initial regime similar to mechanical metamaterials without the phase transitions. The softening observed in the constitutive response at large strain (stage II) is mostly due to the debonding between the polymer and the magnets (SI Appendix, Fig. S7), contributing to the enhanced hysteresis in elasto-magnetic metamaterials with circular pores.
To further explore the relationship between the structure and constitutive response, we measure the loading and unloading response for materials as a function of magnetic interaction parameter (Q), pore shape (a0/b0), and ligament thickness (w0) (Fig. 2C). For example, for elasto-magnetic metamaterials with an attractive magnetic interaction (Q > 0), an elliptical pore shape (a0≪b0) with relative compliant responses at small strain and a relatively thin ligament (w0≪L0), the phase transitions are induced, thus creating the stress plateau in loading and an enhanced hysteretic response upon unloading. A mathematical framework to describe the materials structures prone to these transitions would be advantageous for systematically programming materials with prescribed energy dissipative and recovery modes.
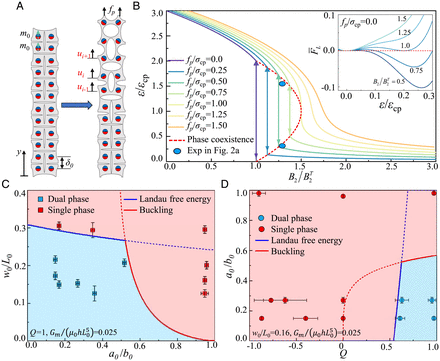
To understand how the internal geometry and the magnetic interaction affect the phase transitions and the constitutive responses in elasto-magnetic metamaterials, we develop an analytical model described in Fig. 3A. Following Landau’s analysis of phase transitions (36), we construct a Landau free energy FL, which is the effective Hamiltonian of the system (SI Appendix, section 3), based on local equilibria:[2]where ui is the displacement of the ith magnet; σs(εi) is the stress–strain relation of the mechanical metamaterials without magnetic domains; Gm is the coefficient for the magnetic interaction; δ0 is the center-to-center distance between two neighboring magnets in the closed phase; and h is the thickness of the sample. The constitutive responses of the mechanical metamaterials and the magnets are adopted from the measurements shown in SI Appendix, Fig. S2. We trade the details of the “microscopic” degree of freedom (e.g., the displacement of each magnet ui) to a coarse-grained continuum field ε, which is a continuous limit of εi in the “macroscopic” scale and serves as the order parameter for the phase transitions. We can rewrite the equilibrium equation (Eq. 2) to the continuum limit and calculate the Hamiltonian of the elasto-magnetic metamaterials (SI Appendix, section 3 for details) per-unit volume (H(ε, dε/dy)) under the external force fp as the following:[3]where , , , and γ is the dummy variable for the integration. The closed and open correspond to the order parameters ε∼0 and ε > 0, respectively. We focus on the vicinity of the phase transitions, where the Landau free energy is expanded as an analytical polynomial function of ε∼0. To a first-order approximation, we expressed the stress–strain relation in the mechanical metamaterials as σs(ε) = C1ε + C3ε3, which captures the sign change in stresses as the deformation switches from tension to compression. Here, we drop the even order term in σs, assuming the strain energy is symmetric with strain ε under tension and compression. The dependence of the parameters C1 and C3 upon metamaterial geometry is fitted to the experiments through linear functions for simplicity. We note that the accuracy of the stress–strain relation can be improved by adding more terms to the fitting functions; however, the underlying symmetry and the physics at phase transitions is altered (SI Appendix, section 4). Therefore, the Landau free energy density is written as the following:[4]where B1 = fp, B2 = (km + C1), B3 = βm/2, and B4 = C3. We neglect the term αm(dε/dy)2/2, as it is positive and serves as an energy penalty to keep ε(y) smooth without forming two phases alternatively. Remarkably, the Landau free energy for elasto-magnetic metamaterials under external loading is similar to liquid crystal elastomers undergoing the nematic-to-isotropic phase transitions under external fields (37, 38). Based on the Landau-de Gennes theory, we expect the closed-to-open phase transitions to echo the first-order phase transitions observed in liquid crystal elastomers (39). Minimizing Eq. 4 to ε and normalizing by the critical coefficient values (40), the equilibrium condition for different phases is the following:[5]where, , and are the mechanical critical points satisfying (ε) = (ε) = (ε) = 0, and . In Fig. 3B, the scaled strains ε/εcp are plotted as a function of , which is the reduced parameter for the coupling between the magnetic interaction and the elastic constitutive response, with different external forces fp/σcp. An open phase (ε/εcp > 1) is reached with a repulsive or weakly attractive magnetic interaction, as < 1. When the attractive magnetic interaction increases (), a closed phase (ε∼0) is favored. Without external force (fp = 0), the absolute minimum of the free energy density is located at ε = 0 for strongly attractive magnets. As the interactions weaken, a metastable minimum with εm > 0 appears. At , the absolute minimum at ε = 0 jumps discontinuously to εm, causing the first-order phase transitions (Fig. 3B, Inset). The points around the transition indicate the coexistence of both phases (arrows in Fig. 3B). For an external force fp > 0, the closed pore phase with ε = 0 no longer exists, and the strain after the phase transitions decreases. The strains at phase coexistence are related to the external force, , and these conditions are plotted with dashed lines for different external forces in Fig. 3B. As the external force increases, the discontinuous jumping of the strain in the phase transitions reduces. The closed-to-open phase transformation is of second order when fp = σcp. The phase transitions disappear as fp > σcp, as observed in Fig. 2A, when the stress is larger than the plateau stress. We also mark the experimental data for phase coexistence with solid circles in Fig. 3B, where the metamaterials experience a closed-to-open phase transition shown in Fig. 2A (SI Appendix, section 4). The Landau free energy analysis captures the discontinuous phase transitions for the elasto-magnetic metamaterials, agreeing with the experiments.
Phase transitions map in elasto-magnetic metamaterials. (A) Schematic of metamaterials with attractive interaction undergoing phase transitions. The metamaterial undergoes the closed-to-open phase transitions with the external force fp. (B) Equilibrium condition of two phases in elasto-magnetic metamaterials under different external forces. The solid circles are the experimental data for the metamaterials with the closed-to-open phase transitions in Fig. 2A. Inset: the scaled Landau free energy density of the metamaterials with different magnetic interactions and zero external forces. Phase diagram of metamaterials with (C) a fixed magnet orientation (Q = 1) and (D) a fixed ligament thickness (w0/L0 = 0.16). The boundaries between the single and the dual phases are determined by the Landau free energy and the ligament buckling conditions. The solid symbols are experimental results.
We construct a phase diagram to compare our model predictions with the experiments and illustrate how internal structures and magnetic interactions control phases in elasto-magnetic metamaterials. The critical condition for the first-order phase transitions in elasto-magnetic metamaterials is determined with zero external force, fp = 0,[6]
In Fig. 3 C and D, we plot the phase diagram for a fixed magnetic moment direction (Q = 1) and a fixed ligament width (w0/L0 = 0.16), respectively. The scaled magnetic strength for the Neodymium magnet is determined by its magnetic moment and the magnetic permeability (SI Appendix, section 2). As shown in Fig. 3C, under a fixed magnet orientation (Q = 1), the metamaterials show a dual phase (blue symbols) with elliptical pore shapes and a small ligament thickness (w0/L0 < 0.25). On the other hand, the single open phase (red symbols) is observed for metamaterials with circular pore shapes and thick ligaments. Eq. 6 delineates the phase boundary (blue line) based on the Landau free energy, which is accurate for elliptical pores with a0/b0 < 0.5. However, it overestimates the critical conditions for phase transitions as a0/b0 approaches 1.
Deviation from the Landau free energy is observed in elasto-magnetic metamaterials with circular pores. In these cases, the slender ligament connecting the neighboring circular pores buckles to form a closed phase instead of bending. To account for this alternative deformation path, we adopt the Euler buckling criterion and predict compressive load for the ligament buckling as . Here, we model the ligament as a simply supported Euler beam with length L0 and bending stiffness Cb (23). The applied compressive force in the ligament without external loading is dictated by the strength of the magnetic interaction: Fm = Gm. The phase boundary based on ligament buckling is determined by Fcr = Fm, shown with a red line in Fig. 3C, which intersects with the line from Eq. 6 at a0/b0 = 0.53. The region enclosed by both criteria (solid lines) in the phase diagram represents the conditions for metamaterials with a dual phase that supports phase transitions. As indicated by comparing with the experimental results, the phase diagram constructed by the Landau free energy and ligament buckling captures the boundary between the dual and single phase in elasto-magnetic metamaterials (Fig. 3 C and D).
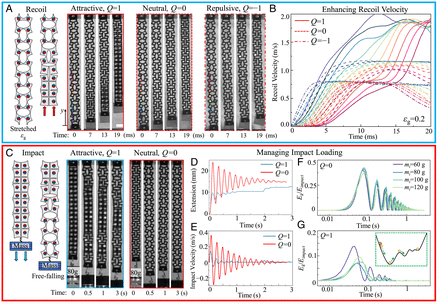
We demonstrate the capacities enabled by the phase transformation in high-rate deformation through dynamic recoil and impact experiments. As shown in Fig.4A, the recoil of vertically hung metamaterials without any external guiding constraints is studied. Out-of-plane bending is suppressed as the metamaterials thickness (h) is much larger than ligament width, h∼3w0. High-speed images (Photron Fastcam APX RS, 10,000 frames per second [fps]) of the recoiling metamaterials with different magnetic interactions are shown in Fig. 4A. The metamaterials (w0 = 1 mm and a0 = 0.17b0) are stretched to the same deformed length with εg = 0.2, and recoiling is initiated by a trigger at time t = 0 ms along the y-direction. We track the position of the magnet via markers placed in the metamaterials (Fig. 4A). The positions corresponding to the color markers in metamaterials with different magnetic interactions (Q = 1, 0, and −1) are measured against the recoil time (SI Appendix, Fig. S17). The recoil velocities based on the time derivative of the displacements are compared in Fig. 4B. The repulsive (Q = −1) and neutral interactions (Q = 0) share similar dynamic responses as they are mainly powered by the ligaments’ elastic deformation (SI Appendix, section 5). The repulsive magnetic interaction also enforces an opposing force in the recoiling direction, reducing the elastic recoil velocity by ∼30% compared to the recoil for metamaterials with Q = 0. By contrast, the metamaterials with attractive interactions experience a phase transformation during recoil, leading to a rapid collapse of the pores (Movie S3). The propagation of the phase transitions, superimposed with the elastic recoil, nearly doubles the elastic recoil velocity. For the metamaterial with circular pores (w0 = 1 mm and a0 = 0.97b0), which predictably only supports the open phase even with the attractive magnetic interaction (Q = 1), the effect of the magnetic interactions on the recoil velocity is much smaller, normally less than 10% (SI Appendix, Fig. S18). Therefore, the propagation of the phase transitions in the metamaterials is responsible for the enhanced high–strain-rate energy release in dynamic recoil.
High–strain-rate deformation of the phase-transforming metamaterials with elliptical pores (w0 = 1 mm and a0 = 0.17b0). (A) Dynamic recoil in metamaterials with different magnetic interactions. (B) Recoil velocity in metamaterials corresponding to the color markers in (A) over time. (C) Free-falling mass impact in metamaterials with different magnetic interactions. (D) The displacement of the impact mass (or the extension of the metamaterials) over time. (E) The vibrational velocity after impact. (F) The ratio of kinetic energy to the total impact energy for metamaterials without the magnetic interaction (Q = 0). (G) The ratio of kinetic energy to the total impact energy for elasto-magnetic metamaterials with Q = 1. Inset: Schematic for energy barriers created by the phase transitions in impact.
While the programmed phase transitions in elastic recoil harness latent energy to access enhanced recoil velocities, programmed phase transitions can also enhance energy dissipation during high-speed impact events. We demonstrate this through a simple experiment designed to measure the dampening response of the metamaterial with an impacting mass (Fig. 4C). The mass is accelerated by letting it fall freely from a predetermined height. The attached metamaterial (w0 = 1 mm and a0 = 0.17b0) stops its fall through stretching (Fig. 4C and SI Appendix, section 2 for details of experiments). We track the dynamic response of the free-falling mass and the metamaterial through high-speed imaging (1,000 fps). For the metamaterials without magnetic interactions (Q = 0), the system oscillates with the free-falling mass, resembling a damped mass-spring vibration (41), where the impact energy is slowly dissipated (SI Appendix, section 5 and Movie S4). The free-falling mass impact stretches the metamaterial with attractive magnetic interactions (Q = 1), but it ceases vibration over a much shorter timescale, indicating significant dampening capabilities (SI Appendix, section 5 and Movie S5). As shown in Fig. 4C, part of the elasto-magnetic metamaterials undergoes a closed-to-open phase transition. The vibrations here only last for a few periods, accompanying the emergence of the open phase (at t = 0.5 s). The closed-to-open phase transitions govern the subsequent deformation, resulting in an almost quasistatic motion, which is heavily damped. The displacement of an 80-g free-falling mass (or the extension of the metamaterial) and the corresponding velocity are plotted in Fig. 4 D and E.
To further explore the damping mechanism, we perform impact experiments for elasto-magnetic metamaterials with different falling weights, ranging from 60 to 120 g. The energy transfer in the impact is characterized based on the high-speed images, which measures the ratio between the kinetic energy in the mass Ek (through the vibrational velocity) and the gravity potential Eimpact (refer to the maximum extension) for different weights (SI Appendix, Figs. S19B and S20B). As shown in Fig. 4F, more than 40% of the total energy is converted to kinetic energy after impact, leading to high-frequency vibrations that take 0.7 s to dissipate for metamaterials without magnetic interactions (Q = 0). The energy conversion event is governed by the damped oscillation, whose period is about 0.1 s for different falling weights, while the dissipation increases with the impact velocity as the weight grows. For metamaterials with attractive magnetic interactions (Q = 1), the vibration decays rapidly in 0.2 s, with less than 20% of the impact energy converted to kinetic energy (Fig. 4G). The rapid absorption of the impact energy relies on the phase transitions and not on the attractive magnetic interactions, as confirmed with experiments on elasto-magnetic metamaterials with circular pores (SI Appendix, section 5). In these circular pore metamaterials with Q = 1, the damped harmonic vibration upon impact is similar to the metamaterials with Q = 0 (SI Appendix, Fig. S21).
Compared to the traditional impact absorption that relies on internal friction and viscoelastic material responses, the damping mechanism in elasto-magnetic metamaterials offers multiple energy barriers through the phase transitions that are activated upon impact. We illustrate the proposed mechanism in the inset of Fig. 4G. The movements of the sphere represent the vibration after impact. Additional energy barriers emerge as the metamaterials transform from a closed to an open phase. The modulated energy landscape dramatically reduces the maximum impact velocity, leading to fast and efficient damping compared to traditional materials (10, 22). While the current phase diagram framework provides insight into how to design an appropriate metamaterial for achieving these dampening responses, further research is required to quantitatively predict the dynamic performance. In particular, inertial and multiphase wave propagation dynamics must be incorporated within the phase framework.